| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- graph
- Stack
- java
- BinaryTree
- 버블정렬
- Tomcat
- 리스트
- 알고리즘
- MariaDB
- aws
- ec2
- Recursion
- 웹서버
- 트리
- spring
- BinarySearchTree
- algorithm
- 그래프
- 큐
- 자료구조
- web
- ADT
- bubblesort
- C
- C언어
- Queue
- datastructure
- heap
- 이진탐색트리
- data structure
- Today
- Total
Min'sLog
(자료구조) 간단한 정렬 알고리즘 3가지 (버블 정렬,선택 정렬,삽입 정렬) 본문
● 정렬(sort) => 탐색(search)을 용이하기 위해 사용 한다.
= 어떠한 기준을 가지고 정렬된 대상을 효율적으로 탐색할 것인가
- 단순한 정렬 알고리즘 : 구현이 용이한 반면 성능이 만족스럽지 않다.
- 복잡한 정렬 알고리즘 : 구현이 복잡하지만 성능이 만족스럽다.
복잡한 정렬 알고리즘은 성능이 중요할때, 공통적으로 사용하기위해 라이브러리화 하여 사용하는 케이스가 많고,
간단한 정렬 알고리즘은 구현이 간단한 만큼, 정렬대상(데이터)이 많지 않을 경우 간편히 구현해서 사용할 수 있는 장점
이 있다.
1. 버블 정렬 (Bubble Sort)
이전 포스팅중 버블 정렬에 대한 설명 및 구현이 있었기 때문에 간략히만 설명하면
수열중 양옆의 수를 계속 비교하여 우선순위별로 비교해 끝수까지 비교를 하면 최 우측에 완전히 정렬된 수가 정렬된다.
그렇게 수열 n개를 n-1번 비교하여 자리를 이동하고, n-1,n-2,n-3...1 까지 자릿수까지 해당 비교반복을 하면 최종적으로
정렬이 완료된다.
○ 구현 코드
#include <stdio.h>
void BubbleSort(int arr[], int len){
int i,j,tmp;
for(i=0;i<len-1;i++){ // n-1 번 자릿수까지 반복
for(j=0;j>(len-i)-1;j++){ // 실제 비교 및 위치 Swap 이 일어나는 구간
if(arr[j]>arr[j+1]){
tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
}
}
}
int main(void){
int arr [4] = {4,3,2,1}
BubbleSort(arr, sizeof(arr)/sizeof(int));
for(i=0; i<4; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}
○ 버블정렬 성능(빅오) : O(n^2)
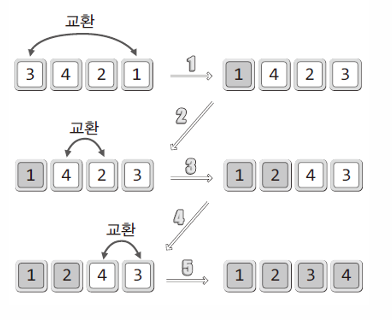
2. 선택 정렬
별도의 메모리 공간을 갖는다.(정렬대상 배열과 같은 크기)
우선순위가 높은 것을 별도 메모리공간에 저장해야 하는 정렬 방법이다.

해당 방식을 개선하여 , 별도의 메모리 공간 쓰지 않고
현재 지정된 인덱스를 고정하고, 우선순위가 높은 인덱스를 저장하여 수열의 끝까지 비교한후
가장 큰 인덱스를 큰 순환의 지정된 인덱스 위치의 자리와 swap 한다.
○ 구현 코드
#include <stdio.h>
void SelectionSort(int arr[],int len){
int i,j,maxIdx,tmp;
for(i=0;i<len-1;i++){ //선택된 idx 의 최종 정렬을 결정하는 순환
maxIdx = i;
for(int j=i+1;j<len;j++){ // 순환은 i+1 번 부터 전체 순회하여 maxIdx 를 결정
if(arr[j]<arr[maxIdx]){ // j인덱스가 우선순위가 높은 경우 maxIdx 를 j로 변경
maxIdx = j;
}
}
tmp = arr[i];
arr[i] = arr[maxIdx];
arr[maxIdx] = tmp;
}
}
void main(void){
int arr[4] = {3,4,1,2}
SelectionSort(arr,sizeof(arr)/sizeof(int));
for(int i=0; i<4;i++){
printf(arr[i]);
}
printf("\n");
}
○ 선택정렬 성능(빅오) : O(n^2)
3. 삽입 정렬
- 1. 정렬이 완료된 영역과 정렬이 안된 영역을 구분해둔다.
- 2. 정렬이 되지 않은 영역에서 데이터를 정렬된 영역으로 넣어 정렬 및 영역을 확장하는 방식이다.
구현시,
비교대상은 뒤로 한칸씩 밀어내면서(이동) 자리를 찾는 경우 그 위치 인덱스로 정렬할 수열을 집어 넣는다.

○ 구현 코드
#include <stdio.h>
void InsertionSortPr(int arr,int len){
int i,j,tmp,insData;
for(i=1;i<n;i++){
insData = arr[i]; // 정렬 대상 저장
for(j=i-1;j>=0;j--){
if(arr[j]>insData){
arr[j+1] = arr[j]; // 비교 대상 뒤로 한칸 밀어준다.
}else break;
}
arr[j+1] = insData; // 찾은 위치에 정렬 대상 삽입
}
}
void main(void){
int arr[4] = {4,2,3,1};
InsertionSortPr(arr,sizeof(arr)/sizeof(int));
for(int i=0;i<4;i++){
printf("%d",arr[i]);
}
printf("\n");
}
○ 삽입 정렬 성능(빅오) : O(n^2)
'DataStructure' 카테고리의 다른 글
| (자료구조) 퀵 정렬(Quick Sort) (0) | 2024.06.08 |
|---|---|
| (자료구조) 병합 정렬(Merge Sort) (1) | 2024.06.07 |
| (자료구조) Heap 의 개념 및 구현 (0) | 2024.05.31 |
| (자료구조) 수식트리(Expression Tree) 구현 Tree(4) (0) | 2024.05.21 |
| (자료구조) 이진트리의 순회(Traversal) Tree(3) (0) | 2024.05.17 |


