| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- C
- web
- 웹서버
- java
- 이진탐색트리
- C언어
- BinaryTree
- ADT
- spring
- 트리
- BinarySearchTree
- MariaDB
- algorithm
- datastructure
- ec2
- Recursion
- data structure
- 큐
- graph
- bubblesort
- 알고리즘
- Queue
- 그래프
- aws
- 자료구조
- Tomcat
- Stack
- heap
- 버블정렬
- 리스트
- Today
- Total
Min'sLog
(자료구조) 수식트리(Expression Tree) 구현 Tree(4) 본문
● 수식트리란?
이진트리의 일종으로 피연산자와 연산자를 하나의 트리로 구성하는것이다.
중위 표기법은 인간이 인식하기 좋지만, 컴퓨터는 연산자의 우선순위를 고려해야 하기 때문에,
C언어의 컴파일러는 중위 표기법의 수식을 수식트리의 형태로 치환한다.
중위 표기법의 수식을 수식 트리로 변환하는 프로그램의 작성이 목적이다.
예시)

※ 수식트리 -> 수식을 표현하는 하나의 표현 방법
● 수식 트리를 만드는 구성
중위 표기법의 수식을 바로 수식 트리로 표현하기 쉽지 않으므로,
이전 챕터(스택의 활용편)에서 계산기 프로그램을 위해 만들어둔 함수
ConvToRPNExp 함수 (Infix -> PostFix) 를 통해 PostFix로 변환해준다.
변환한 수식을 이진트리와 스택을 활용하여, 수식트리로 변환한다.
● 수식트리의 구현 관련 헤더파일 및 구현할 함수
○ header
#include "BinaryTree2.h" // 이진트리
#include "ListBasedStack.h" // 스택
○ function
BTreeNode * MakeExpTree(char exp[]); // 수식 트리 구성
int EvaluateExpTree(BTreeNode *bt); // 수식트리 계산
void ShowPrefixTypeExp(BTreeNode *bt); // 전위 표기법 기반 출력
void ShowInfixTypeExp(BTreeNode *bt); // 중위 표기법 기반 출력
void ShowPostfixTypeExp(BTreeNode *bt); // 후위 표기법 기반 출력
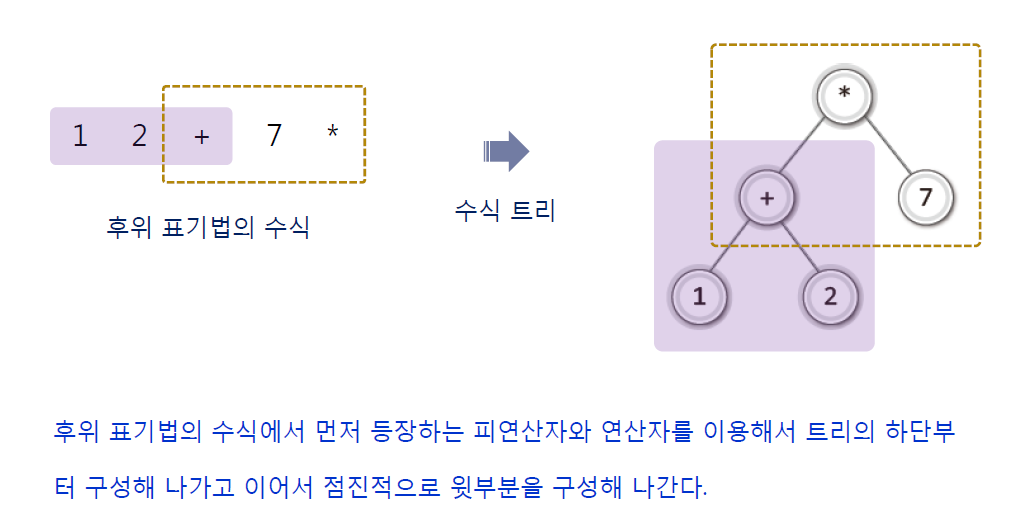
● 수식 트리의 구성 방법
후위 표기법의 수식에서 먼저 등장하는 피연산자와 연산자를 이용해서 트리의 하단부터
구성해 나가고 이어서 점진적으로 윗부분을 구성해 나간다.
순서)
1. 피연산자는 저장한다.
2. 연산자는 노드로 구성한다.
3. 연산자의 left ,right 노드를 연결
4. 서브트리를 피연산자로 인식 시켜서 서브트리로 구성
** 구현 상세
○ 수식트리 구성 : MakeExpTree function
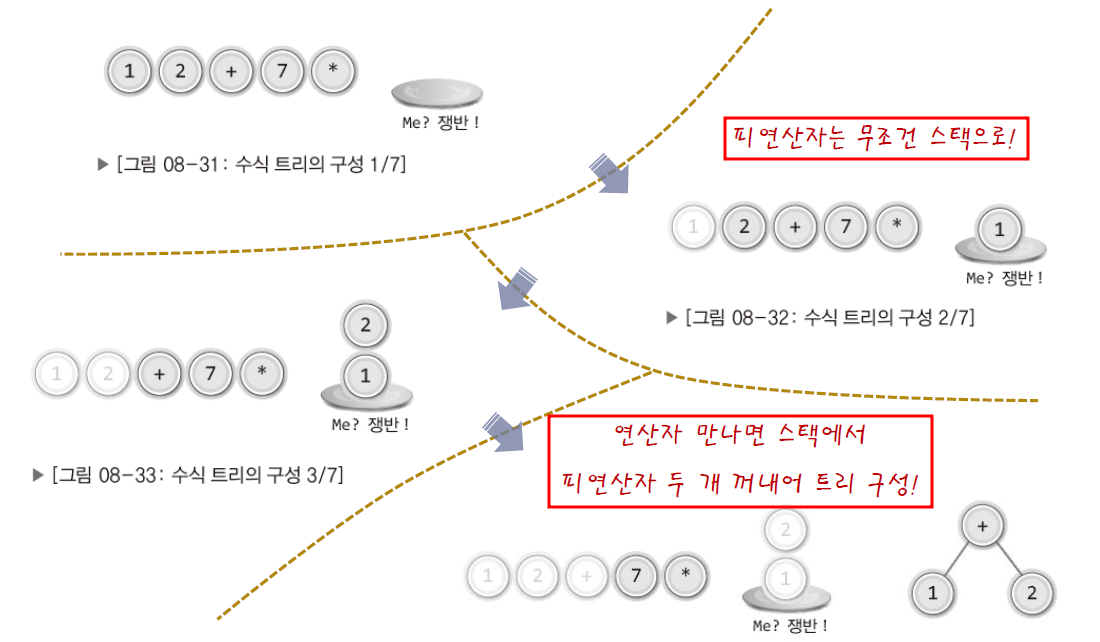
1. 피연산자는 무조건 스택에 쌓는다.
2. 연산자를 만나면 스택에서 피연산자 두개를 꺼내 트리 구성
3. 형성된 트리는 다시 스택에 쌓는다.
(반복...)
결과 값은 스택에 쌓여있다.(1개)
<그림 참조>

<구현코드: MakeExpTree>
BTreeNode * MakeExpTree(char exp[]){
int i;
int expLen = exp.strlen();
Stack st ;
StackInit(&st);
BTreeNode * bn;
for(i=0;i<expLen;i++){
bn = MakeBTreeNode();
if(exp[i].isDigit){
SetData(bn,exp[i]-'0');
}else{
GetLeftSubTree(bn,SPop(&st));
GetRightSubTree(bn,SPop(&st));
SetData(bn,exp[i]);
}
SPush(&st,bn);
}
return Spop(&st);
}
○ 수식트리의 순회
이진트리의 순회와 동일하며, function pointer 를 문자와 숫자를 구분해서 출력하도록 한다.
<function pointer>
void ShowNodeData(int data){
if(0<=data && data <=9)
printf("%d",data); // 피연산자 출력
else printf("%c",data); // 연산자 출력
}
<순회 function>
// 전위
void ShowPrefixTypeExp(BTreeNode * bt)
{
PreorderTraverse(bt, ShowNodeData);
}
//중위
void ShowInfixTypeExp(BTreeNode * bt)
{
InorderTraverse(bt, ShowNodeData);
}
//후위
void ShowPostfixTypeExp(BTreeNode * bt)
{
PostorderTraverse(bt, ShowNodeData);
}
○ 수식 트리의 계산 : EvaluateExpTree
1.트리노드의 left와 right 의 피연산자를 노드의 Data부 연산자와 더해야 한다.
2.하지만 트리의 left /right 가 연산자인 경우가 존재한다(노드가 아닌 서브트리)
3.이를 해결하기 위해서, function을 재귀적으로 구성하여, 말단노드를 찾을시, 해당 결과 값들을 리턴받아 누적 계산하여 결과 값을 반환하도록 구성한다.
<계산 EvaluateExpTree>
int EvaluateExpTree(BTreeNode * bt){
if(bt->left==NULL&&bt->right==NULL){ //탈출조건 : left 와 right 가 NULL인 경우 피연산자 반환
return GetData(bt);
}
int a = EvaluateExpTree(bt->left); // 재귀 호출 left
int b = EvaluateExpTree(bt->right); // 재귀 호출 right
switch(GetData(bt)){
case : '+'
return a+b;
case : '-'
return a-b;
case : '*'
return a*b;
case : '/'
return a/b;
}
return 0;
}'DataStructure' 카테고리의 다른 글
| (자료구조) 간단한 정렬 알고리즘 3가지 (버블 정렬,선택 정렬,삽입 정렬) (0) | 2024.06.01 |
|---|---|
| (자료구조) Heap 의 개념 및 구현 (0) | 2024.05.31 |
| (자료구조) 이진트리의 순회(Traversal) Tree(3) (0) | 2024.05.17 |
| (자료구조) 이진트리(BinaryTree) 개념 및 구현 Tree(2) (0) | 2024.05.14 |
| (자료구조) 트리의 정의 및 용어 정리 - Tree(1) (0) | 2024.05.12 |




