| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 이진탐색트리
- algorithm
- heap
- 웹서버
- ec2
- bubblesort
- 버블정렬
- data structure
- 자료구조
- BinarySearchTree
- graph
- C언어
- BinaryTree
- web
- java
- Recursion
- datastructure
- 리스트
- 트리
- C
- ADT
- MariaDB
- 큐
- 그래프
- Tomcat
- Stack
- spring
- aws
- Queue
- 알고리즘
- Today
- Total
Min'sLog
(자료구조) 그래프(Graph)란? -그래프(1) 본문
● 그래프란?
정점(V, vertext)과 그 정점을 연결하는 간선(E, edge)의 집합 / 정점과 간선을 하나로 모은 자료구조이다.
그래프 (G)의 정점의 집합 -> V(G) 로 표시,
그래프 (G)의 간선의 집합 -> E(G) 로 표시한다.

● 그래프의 종류
○ 무방향 그래프(Undirected Graph)
무방향 그래프는 두 정점(vertext)을 잇는 간선(edge)의 방향이 없는 그래프이다.(간선을 표현할때 () 소괄호로 표현)
ex)
V(G1) = {동수,지민,지율,민석,수정,정희)
E(G1) = {(동수,지민),(동수,지율),(지율,민석),(지민,민석),(민석,수정),(민석,정희),(수정,정희)}

○ 방향 그래프(Directed Graph)
방향 그래프는 두 정점을 잇는 간선의 방향성이 존재하는 그래프이다. (간선으로 표현할 때, <> 꺽쇠로 표현)
ex)
V(G2) = {동수,지민,지율,민석,수정,정희}
E(G2) = {<동수,지율>,<지율,민석>,<민석,지민>,<지민,동수>,<수정,민석>,<민석,정희>,<정희,수정>}

○ 완전 그래프(Complete Graph)
완전그래프는 한정점에서 다른 모든 정점과 연결되어 있는 최대 간선이 존재하는 그래프이다.
무방향 완전그래프의 경우 최대 간선의 수 : n(n-1)/2 개
방향 완전 그래프의 경우 최대 간선의 수 : n(n-1) 개
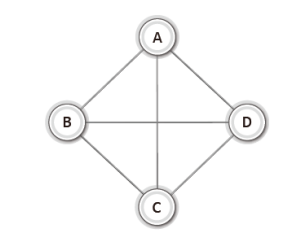
○ 부분 그래프(Sub Graph)
부분 그래프는 기존 그래프에서 일부 정점이나 간선등이 제외된 그래프를 말한다.

○ 가중 그래프(Weight Graph)
가중 그래프는 정점(vertext)를 연결하는 간선에 비용이나 가중치를 할당한 그래프를 말한다.

● 그래프(Graph)와 관련된 용어
- 정점(vertex): 위치라는 개념. (node 라고도 부름)
- 간선(edge): 위치 간의 관계. 즉, 노드를 연결하는 선 (link, branch 라고도 부름)
- 인접 정점(adjacent vertex): 간선에 의해 직접 연결된 정점
- 정점의 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
⇒ 무방향 그래프에 존재하는 정점의 모든 차수의 합 = 그래프의 간선 수의 2배
- 진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (내차수 라고도 부름)
- 진출 차수(out-degree): 방향 그래프에서 외부로 향하는 간선의 수 (외차수 라고도 부름)
⇒ 방향 그래프에 있는 정점의 진입 차수 또는 진출 차수의 합 = 방향 그래프의 간선의 수(내차수 + 외차수)
- 경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
- 단순 경로(simple path): 경로 중에서 반복되는 정점이 없는 경우
- 사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
● 그래프(Graph)의 특징
- 그래프는 네트워크 모델 이다.
- 2개 이상의 경로가 가능하다.
⇒ 즉, 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있다.
- self-loop 뿐 아니라 loop/circuit 모두 가능하다.
- 루트 노드라는 개념이 없다.
- 부모-자식 관계라는 개념이 없다.
- 순회는 DFS나 BFS로 이루어진다.
- 그래프는 순환(Cyclic) 혹은 비순환(Acyclic)이다.
- 그래프는 크게 방향 그래프와 무방향 그래프가 있다.
- 간선의 유무는 그래프에 따라 다르다.
● 그래프의 구현 방식
○ 인접 행렬 기반의 구현
인접 행렬은 N*N Boolean Matrix 로 matrix[i][j] 가 true일때, i -> j로의 간선이 있다는 뜻이다.
grMatrix[i][j] = 1; // i -> j 에 간선이 존재
grMatrix[i][j] = 0; // i -> j 에 간선이 존재하지 않음
- 0과 1을 이용한 정수 행렬을 활용할 수도 있다.
- 정점(노드)의 개수가 N인 그래프를 인접 행렬로 표현
⇒ 간선의 수와 무관하게 n^2개의 메모리 공간을 필요로 한다.
- 무방향 그래프를 인접 행렬로 표현하면 이 행렬은 대칭 행렬(Symmetric Matrix)이 된다.

○ 인접 리스트 기반의 구현
인접 리스트(Adjacency List)로 그래프를 표현하는 것이 가장 일반적인 방법이다.
- 모든 정점을 인접 리스트에 저장한다. (정점을 저장)
⇒ 배열과 배열의 각 인덱스마다 존재하는 또 다른 리스트(배열,arrayList, LinkedList 등..)를 이용해서
인접 리스트를 표현.
⇒ 정점의 번호만 알면 이 번호를 배열의 인덱스로 하여 각 정점의 리스트에 쉽게 접근할 수 있다.
// 리스트 기반 Graph 구조체 (예시)
typedef struct _graph{
int numV; // 정점의 수
int numE; // 간선의 수
List * adjList; // 간선의 정보
} Graph;
// 초기화
void GraphInit(Graph * pg, int nv){
int i;
pg->adjList = (List*)malloc(sizeof(List)*nv);
pg->numV = nv;
pg->numE = 0;
// 정점의 수만큼 생성된 리스트들을 초기화
for(i=0;i<nv;i++){
ListInit(&(pg->adjList[i]));
}
}
- 무방향 그래프의 경우 간선은 두번 저장된다.
ex) (A,B) 인 경우, A : B , B : A 두개가 생성.

○ 인접 리스트와 인접 행렬 중 선택방법.
1. 인접리스트를 사용 -> 그래프 내 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 인 경우
장점 : 어떤 노드에 인접한 노드를 쉽게 찾을 수 있다. O(N+E) : 인접 리스트 전체를 조사
단점 : 어떤 정점 i의 리스트에 있는 노드의 수 정점 차수를 알기 위해서는 정점의 차수만큼의 시간 필요
2. 인접행렬을 사용 -> 그래프에 간선이 많이 존재하는 밀집(Dense Graph인 경우
장점 : 두 정점을 연결하는 간선의 존재 여부 (M[i][j]) 를 O(1) 안에 탐색 가능하다.
정점의 차수는 O(N)안에 찾을 수 있다. : 인접 배열 i번째 행 또는 열을 모두 더함.
단점 : 어떤 노드에 인접한 노드들을 찾기 위해서는 모든 노드를 전부 순회해야 한다.
그래프에 존재하는 모든 간선의 수는 O(N^2)안에 탐색 : 인접 행렬 전체를 조사해야 함.
'DataStructure' 카테고리의 다른 글
| (자료구조)너비 우선 탐색 (Breadth-First-Search) - 그래프(3) (0) | 2024.07.11 |
|---|---|
| (자료구조) 깊이 우선 탐색(DFS) - 그래프(2) (0) | 2024.07.06 |
| (자료구조) 해시 테이블(Hash Table) (0) | 2024.06.30 |
| (자료구조) AVL 트리의 이해와 구현 (0) | 2024.06.21 |
| (자료구조) 이진 탐색 트리(BST) (0) | 2024.06.15 |




